Borel measure
In mathematics, specifically in measure theory, a Borel measure is defined as follows: let X be a locally compact Hausdorff space, and let 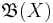 be the smallest σ-algebra that contains the open sets of X; this is known as the σ-algebra of Borel sets. Any measure μ defined on the σ-algebra of Borel sets is called a Borel measure. Some authors require in addition that μ(C) < ∞ for every compact set C. If a Borel measure μ is both inner regular and outer regular, it is called a regular Borel measure. If μ is both inner regular and locally finite, it is called a Radon measure. Note that a locally finite Borel measure automatically satisfies μ(C) < ∞ for every compact set C.
be the smallest σ-algebra that contains the open sets of X; this is known as the σ-algebra of Borel sets. Any measure μ defined on the σ-algebra of Borel sets is called a Borel measure. Some authors require in addition that μ(C) < ∞ for every compact set C. If a Borel measure μ is both inner regular and outer regular, it is called a regular Borel measure. If μ is both inner regular and locally finite, it is called a Radon measure. Note that a locally finite Borel measure automatically satisfies μ(C) < ∞ for every compact set C.
On the real line
The real line R with its usual topology is a locally compact Hausdorff space, hence we can define a Borel measure on it. In this case, 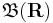 is the smallest σ-algebra that contains the open intervals of R. While there are many Borel measures μ, the choice of Borel measure which assigns
is the smallest σ-algebra that contains the open intervals of R. While there are many Borel measures μ, the choice of Borel measure which assigns ![\mu([a,b])=b-a](/2012-wikipedia_en_all_nopic_01_2012/I/bf767e1e60b0c828f12be60d726c6e86.png) for every interval
for every interval ![[a,b]](/2012-wikipedia_en_all_nopic_01_2012/I/2c3d331bc98b44e71cb2aae9edadca7e.png) is sometimes called "the" Borel measure on R. In practice, even "the" Borel measure is not the most useful measure defined on the σ-algebra of Borel sets; indeed, the Lebesgue measure
is sometimes called "the" Borel measure on R. In practice, even "the" Borel measure is not the most useful measure defined on the σ-algebra of Borel sets; indeed, the Lebesgue measure  is an extension of "the" Borel measure which possesses the crucial property that it is a complete measure (unlike the Borel measure). To clarify, when one says that the Lebesgue measure
is an extension of "the" Borel measure which possesses the crucial property that it is a complete measure (unlike the Borel measure). To clarify, when one says that the Lebesgue measure  is an extension of the Borel measure
is an extension of the Borel measure  , it means that every Borel measureable set E is also a Lebesgue measureable set, and the Borel measure and the Lebesgue measure coincide on the Borel sets (i.e.,
, it means that every Borel measureable set E is also a Lebesgue measureable set, and the Borel measure and the Lebesgue measure coincide on the Borel sets (i.e.,  for every Borel measureable set).
for every Borel measureable set).
References
- J. D. Pryce (1973). Basic methods of functional analysis. Hutchinson University Library. Hutchinson. p. 217. ISBN 0-09-113411-0.
- Alan J. Weir (1974). General integration and measure. Cambridge University Press. pp. 158–184. ISBN 0-521-29715-X.